函数有极限的三要素 函数有极限的三要素是什么

函数极限存在的条件：1、单调有界准则。函数在某一点极限存在的充要条件是函数左极限和右极限在某点都存在且相等。如果左右极限不相同、或者不存在。则函数在该点极限不存在。

文章目录：

1. 函数极限存在的条件是什么?
2. 一个函数有极限需满足哪些条件?
3. 一个函数有极限需满足哪些条件?
4. 极限存在的条件是什么?

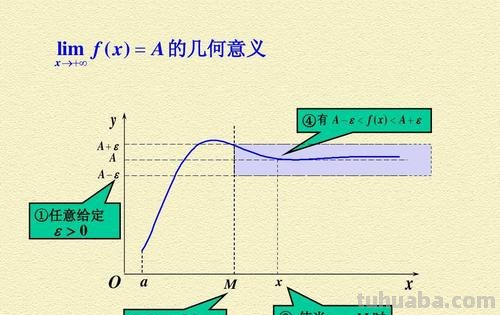
一、函数极限存在的条件是什么?

函数极限存在的条件：

一、单调有界准则。

二、夹逼准则，如能找到比目标数列或者函数大而有极限的数列或函数，并且又能找到比目标数列或者函数小且有极限的数列或者函数，那么目标数列或者函数必定存在极限。

函数在某一点极限存在的充要条件是函数左极限和右极限在某点相等。如果左右极限不相同、或者不存在。则函数在该点极限不存在。即从左趋答液向于所清颂物求点时的极限值和从右趋向于所求点的极限值相等。

扩展资料：

在运用以上两条去求函数的极限时尤需注意以下关键之樱中点。一是先要用单调有界定理证明收敛，然后再求极限值。二是应用夹挤定理的关键是找到极限值相同的函数 ，并且要满足极限是趋于同一方向 ，从而证明或求得函数 的极限值。

第一：因式分解，通过约分使分母不会为零。

第二：若分母出现根号，可以配一个因子使根号去除。

第三：以上我所说的解法都是在趋向值是一个固定值的时候进行的，如果趋向于无穷，分子分母可以同时除以自变量的最高次方。（通常会用到这个定理：无穷大的倒数为无穷小）

参考资料来源：百度百科-函数极限

函数极限存在的条件：

1、单调有界准则。函数在某一点极限存在的充要条件是函数左极限和右极限在某点都存在且相型备等。如果左右极限不相同、或者不存在。则函数在该点极限不存在。即从左趋向于所求点时的极限值和从右趋向于所求点的极限值相等。

2、夹逼准则，如能找到比目标版数列或者函数权大而有极限的数列或函数，并且又能找到比目标数列或者函数小且有极限的数列或者函数，那仿租巧么目标数列或者函数必定存在极限。

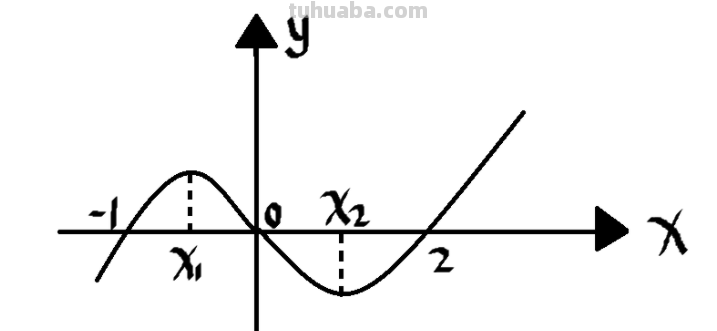
扩展资料：

当分母等于零时，就不能将趋向值直接代入分母，可以通过下面几个小方法解决：

第一：因式分解，通过约分使分母不会为零。

第二：若分母出现根号，可以配一个因子使根号去除。

第三：以上我所说的解法都是在趋向值是一个固定值的时候进行的，如果趋向于无穷，分子分母可以同时除以自变量的最高次方。备键（通常会用到这个定理：无穷大的倒数为无穷小）。

二、一个函数有极限需满足哪些条件?

函数极限是高等数学最基本的概念之一，导数等概信隐念都是在函数极限的定义上完成的。函数极限性质的合理运用。常用的函数极限的性斗清质有函数滑销厅极限的唯一性、局部有界性、保序性以及函数极限的运算法则和复合函数的极限等等。

如果函数在某虚行碰点的左右极限存在并且相等，那么该函数在该点的极限存在。

单调有界准则：单调增加（减少）有上（下）界的数列必定收敛。

在运用以上两条去求函数的极限时尤需注意以下关键之点。一是先要用单调有界定理证明收敛，然后再求极限值。二是应用夹挤定理的关键是找到极限值相同的函数 ，并且要满足极限是趋于同一方向 ，从而证明或求得函数 的极限值。

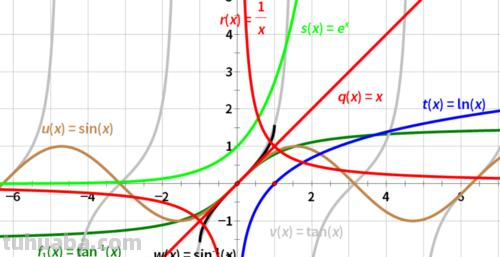
扩展资料：

当分母等于零时，就不能将趋向值直接代带芦入分母，可以通过下面几个小方法解决：

第一：因式分解，通过约分使分母不会为零。

第二：若分母出现根号，可以配一个因子使根号去除。

第三：以上我所说的解法都是在趋向值差谈是一个固定值的时候进行的，如果趋向于无穷，分子分母可以同时除以自变量的最高次方。（通常会用到这个定理：无穷大的倒数为无穷小）

当然还会有其他的变形方式，需要通过练习来熟练。

如果函数在某点的左右极限存在并且相等御亩,那么该函数在该点的极限存在.例如,分段函数f(x)=x^2+2x-3

x<2

=5

x=2

=x^3-3

x>2在x=2这一点极限存在,等镇码森于模派5

三、一个函数有极限需满足哪些条件?

如果函数在镇码森某点的左右极限存在并且相等,那么该函数在该点的极限存在.例如模派,分段函数f(x)=x^2+2x-3 x<2 =5 x=2 =x^3-3 x>2在x=2这一点极限存在,等御亩于5

这个孝春让问题建议你认真复习下函数极限的定义。

函数在某一点X0有极限我的理解：

设函数f(x)在点x。的空心邻域内有定义，如果存在巧局常数A，对于任意给定的正数ε（无论它多么小），总存在正数δ ，使得当x满足不等式0<|x-x。|<δ 时，对应的函数值f(x)都满足不等式： |f(x)-A|<ε那么常数A就叫做函数f(x)当x→x。时的极森册限。也就是说函数在点X0有极限。

另外也可以这样理解，一个函数在某个点X0有极限，只需要在X0左右极限都存在且相等，而且与该点的函数值没有关系，甚至该点的函数值可以不存在。换句话说，函数某点的极限不一定等于该点的函数值。

只有函数在该点连续时，极限值才等于该点的函数值

四、极限存在的条件是什么?

极限存在的条件：

一、单调有界准则。并租函数在某一点极限存在的充要条件是函bai数左极限和右极限在某点都存在且相等。

如果左右极限不相同、或者不存在。则函数在该点极限不存在。即从左趋向于所求点时的极限值和从右趋向于所求点的极限值相等。

二、夹逼准则，如能找到比目标版数列或者函数权大而有极限的数列或函数，并且又能找到比目标数列或者函数小且有极限的数列或者函数，那么目标数列或者函数必定存在极限。

扩展资料：

在区间（a-ε，a+ε）之外笑蔽毁至多只有N个（有限个）点；所有其他的点xN+1，xN+2，...（无限个）都落在该邻域之内。这两个条件缺一不可，如果一个数列能达到这两个要求，则数列收敛于a。

而如果一个数列碰备收敛于a，则这两个条件都能满足。换句话说，如果只知道区间（a-ε，a+ε）之内有{xn}的无数项，不能保证（a-ε，a+ε）之外只有有限项，是无法得出{xn}收敛于a的，在做判断题的时候尤其要注意这一点。

以上对于函数有极限的三要素的问题的4点解答，由涂画吧（tuhuaba.com）小编收集与互联网，希望对大家有用。