数学卡壳？一张思维导图盘活思路！

你的孩子试过用思维导图解决数学问题吗？当高年级孩子学习努力但成绩停滞，往往问题在于：知识点变难后思路阻塞，知识散落缺乏串联。此时，刷题不如构建思维网络。今天，我们就用一道让不少孩子头疼的初中数学综合题当例子，看看如何借助思维导图，把孩子从听不懂、理不清的困境中拉出来。

一、解决数学应用题

题目是这样的（别怕，我们不解题，只理思路）

在平面直角坐标系中，点A(0, 4)，点B是x轴正半轴上的动点。以线段AB为边，在第一象限内作等边三角形ABC。以点 O(0,0) 为圆心，作半径为2的圆。当圆O与直线 BC有公共点时，求点B横坐标的取值范围。

看到这道题，孩子的感受通常是：条件好多（动点、等边三角形、圆），关系好乱（怎么又有直线又有圆），问题好绕？

接下来我们用知犀思维导图演示一下如何拆解这个题目的思路。

（一）破题拆解

先别想怎么解，而是带着孩子在思维导图中心写下问题，有哪些已知条件，固定条件？目标是什么？题目中哪些点是固定的？哪些是变化的，要不要分类讨论？……

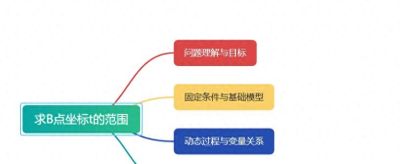
知犀思维导图

（二）拆解

接着，我们可以依据这四大步，深入解决问题，建立新的分支。

第一步，可以利用知犀思维导图整合题目条件，建立第一个主干分支。列出已知条件和目标便于把散落的信息，固定到纸上，建立思考的起点和基石。

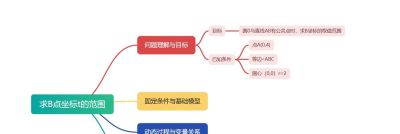
知犀思维导图

第二步，推导

由题目的固定条件，与基础知识，可推导出下一分支

△ABC是等边三角形⟺ ∠ABC=60°，AB=BC=AC

圆O与直线BC有公共点转化为数学语言：圆心到直线的距离 ≤ 半径圆心⟺ d ≤ 2

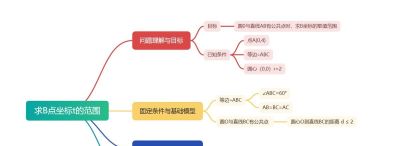
知犀思维导图

（三）思考变量，得出方程

第一步，找到联系桥梁，求直线AB的倾斜角

设动点B坐标(t, 0)，其中 t > 0。利用A(0,4), B(t,0)，可求斜率，得到∠ABO=60°⟺ 直线BC相对于直线AB的倾斜角是固定的±60°。

第二步，继续建立下一级子分支：表达目标距离d。我们需要的是圆心O(0,0)到直线BC的距离d。因此，可以用变量t表示出直线BC的方程。

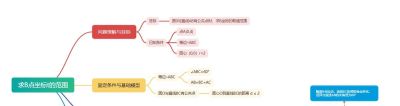
将一个动点B如何引发直线BC方程变化这一抽象的动态逻辑，拆解成三步具体的、可执行的数学操作。思维导图让这个逻辑链条清晰可见，避免思维迷失在动态想象中。

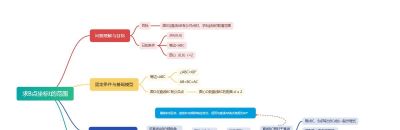
第三步：核心推导

这是最复杂的一步，导图可以引导思维聚焦。

1.在改刚刚的子分支下，继续深入。利用点斜式求直线BC方程。可以推导出直线BC的一般式方程，其系数是包含变量t和三角函数的表达式。

2.将圆心O(0,0)坐标代入点到直线距离公式，得到d关于t的函数表达式：d(t) = 某个含t的表达式

3.此时，导图会清晰地指向一个条件方程：令 d(t) = 2，解出对应的t值。这个t值就是临界值。

知犀思维导图

思维导图把这个抽象的、动态的逻辑关系，变成了一个静态的、可视化的推导路径。孩子可以一步步跟进，每一步都知道我现在在算的是什么，为什么要算这个，避免了在复杂的想象中迷失方向。

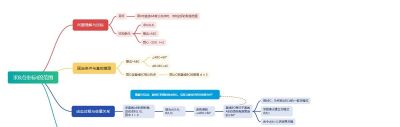
（四）分类讨论，整合结论

在前面的确定直线BC方位时，我们发现等边三角形可以在AB的左侧或右侧，这对应了两种不同的直线BC位置。

在导图中，我们建立两个平行的子分支：

情况1：直线BC在AB一侧。对应一个临界方程，解出一个临界值 t1。

情况2：直线BC在AB另一侧。对应另一个临界方程，解出另一个临界值 t2。

然后分析：在每种情况下，t大于或小于这个临界值时，圆和直线是相交还是相离。

最后，整合两种情况下的取值范围，得到最终答案。

知犀思维导图

通过这个例子，您可以看到，思维导图不仅是在整理一道题，更是在培养孩子结构化思考的底层能力。它把隐性的思考过程变得可视化、可调整，不怕想错。在软件上分支可以随时拖拽、修改、合并。思考不再是写在纸上不能涂改的“终稿”，而是一个可以不断调整、优化的动态过程以及随时复盘的思考框架。不妨就从孩子今晚的一道难题开始，陪他一起画一张思维导图，体验一次思路清晰的感觉吧。