什么是三角形的重心 什么是三角形的重心,垂心,内心,外心,中心

三角形重心是三角形三条中线的交点。当几何体为匀质物体时，重心与形心重合。直角三角形的重心在斜边中点。

文章目录：

1. 什么是三角形的重心?
2. 什么叫三角形的重心?
3. 什么是三角形的重心
4. 三角形重心是什么
5. 什么是三角形的重心?
6. 三角形的重心是什么?

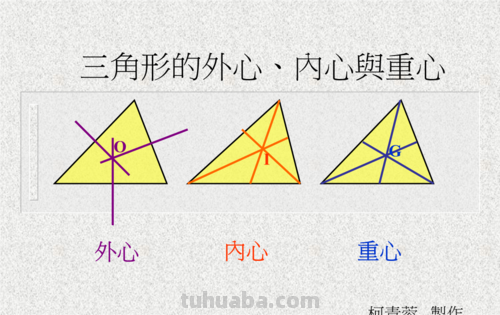
一、什么是三角形的重心?

三角形重心是三角形三条中线的交点。当几何体为匀质物体时，重心与形心重合。直角三角形的重心在斜边中点，等腰三角形的重心是三条高的交点(所有的都是),它和它的中心、内心、外心在同一条直线上,也叫心连心。

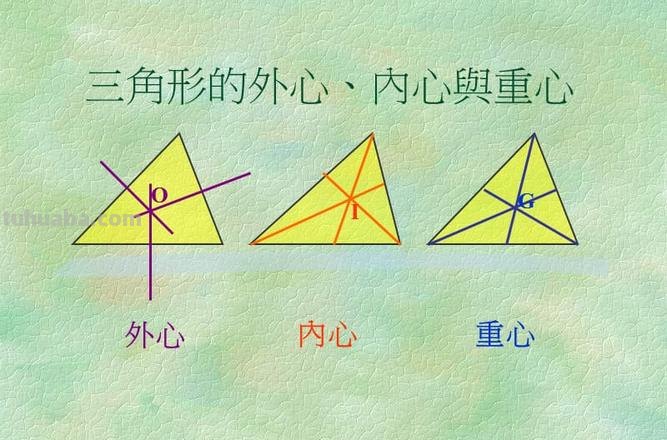
扩展资料：

1、内心是三条角平分线的交点，它到三边的距离相等。

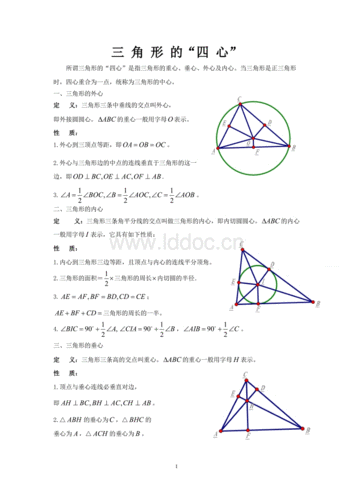
2、外心是三条边垂直平分线的交点，它到三个顶点的距离相等。

3、重心是三条中线的交点，它到顶点的距离是它到对边中点距离的2倍。

4、垂心是三条高的点，它能构成很多直角三角形相似。

5、旁心是一配备个内角平分线与其不相邻的两个外角平分线的交点，它到三边的培茄毁距离相等。

（1）重心和三顶点的连线所构成的三个三角形面积相等；

（2）外心扫三顶点的距离相等；

（3）垂心与三顶点这四点中，任一点是其余三点构成的三角形的垂心；

（4）内心、旁心到三边距离相等；

（5）垂心是三垂足构成的三角形的内心，或者说，三角形的内心是它旁心三角形的垂心；

（6）外心是中点三角形的垂心；

（7）中心也是中点三角形的重心；

（8）三角形的中点三角形的外心也是其垂足三角形的纳森外心。

二、什么叫三角形的重心?

三角形重心是三角磨衫丛形三边中线的交点O。

重心：是在重力场中，规塌碧则而密度均匀物体的重心就是它的瞎樱几何中心。

AD、BE、CF都是平分△ABC面积的三条线，虽然二维平面图形没有重量，但是形象的称之为三角形的重心。

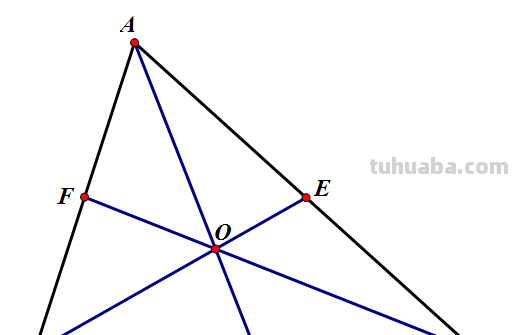
重心:三角形顶点与对边中点的连线交于一点,称为三角虚宴悔形重心;

垂心:三角形各边上的高交于一点,称为三角形垂心;

外心:三角祥森形各边上的垂直平分线交于一点,称为三角形外心;

内心:三角形三内角平分线交于一点,称为三角形内心;

中心:正三角形的重心、垂心、外心、差正内心重合，称为正三角形的中心。

三角形重心带冲的定义是三角形三条中线的交点。

数学上的重心是指三角形的三条中线的交点，其证明定理有燕尾定理或塞瓦定理，应用定理有梅涅劳斯定理、塞瓦定理。

对于均质物体，如在几何形体上具有对称面、对称轴或对称中心蠢派歼，则该物体的重心或形心羡族必在此对称面、对称轴或对称中心上。下面介绍几种常用的确定重心位置的方法。

三角形的重心是三边中线的交点

三、什么是三角形的重心

三角形的重心是三角形三条中线的交点。

当几何体为匀质物体时，重心与形心重合。锐角如首三角形以等边三角形为例，等边三角形的重心亦为垂心，即三角形三条高连线的交点前穗。只有等边三角形的重心与垂心重合，其他三角形无此类情况。

三角形重心到顶点的距离与重心到对边中点的距离之比为2：1。重慧橡卜心和三角形3个顶点组成的3个三角形面积相等。

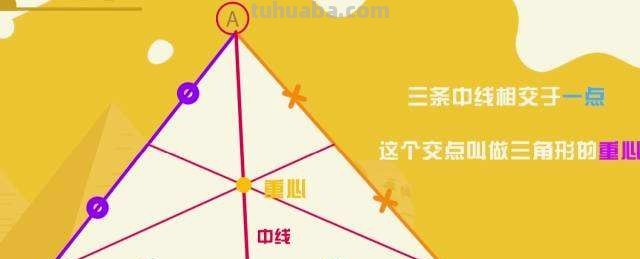
三角形重心的性质

在平面直角坐标系中，重心的坐标是顶点坐标的算术平均，即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)；空间直角坐标系——横坐标：(X1+X2+X3)/3 纵坐标：(Y1+Y2+Y3)/3 竖坐标：（Z1+Z2+Z3）/3。

重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。 重心到三角形3个顶点距离的平方和最小。重心是三角形内到三边距离之积最大的点。

三角形的重心是三角形三条中线的交点。

也就是说，三角形的三条中线的交点就是三角形的重心。

四、三角形重心是什么

三角形顶点到对边中点的连线叫三角形的中线。

三角形的中线就是顶点到对边中点的连线，平分所在边。三角形的三条中线交于一点，这点到顶点的距离是其到对边中点距离的2倍。该点叫做三角形的重心。直角三角形斜边上的中线等于斜边的一半。

三角形的中线是连接三角形顶点和它的对边中点的线段。每个三角形都有三条中线，它们都在三角形的内部  。在三角形中，三条中线的交点是三角形的重心。三角形的三条中线交于一点，这点位于各中线的三分之二处。

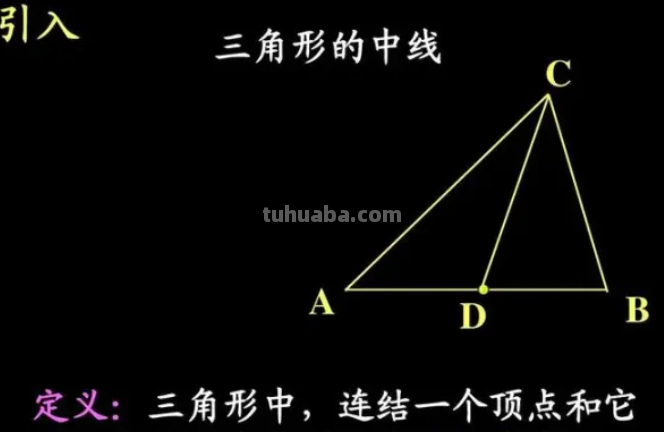
每个三角形都有三条中线，并且它们都在三角形的内部，且三条中线交于一点，这三条中线的交点叫做三角形的重心。每条三角形的中线分得的两个三角形面积相等。三角形的重心将中线分为长度比为1:2的两条线段。在直角三角形中，其斜边上的中线长度等于斜边的一半。

正三角形的中线长度都一样长，且中线、角平分线、高线，三条线互相重合，三线合一。交点为正三角形的中心，“重心”与“中心”较容易混淆，“中心”只存在于正三角形中。

五、什么是三角形的重心?

三角形的三条边上的中线交于一点者氏念，这点叫做核信三角形的重心。

三角形的三条边上的高交于一点，这点叫做三角形的垂心，。

三角形的三个内角的平分线交于一点，这点叫做三角形的内心。

三角形的三条边的垂直平分线交于一点，这点叫做三角形的外心，

正三角形的四心重合，也就是正首困三角形的中心。

六、三角形的重心是什么?

重心是三角形三边中线的交点。重心到顶点的距离与重心到对边中点的距离之比为2：1，重心和三角形3个顶点组成的3个三角形面积相等，重心到三角形3个顶点距离的平方和最小。

三角形重心是三角形三中线的交点。当几何体为匀质物体且重力场均匀时，重心与该形中心重合。

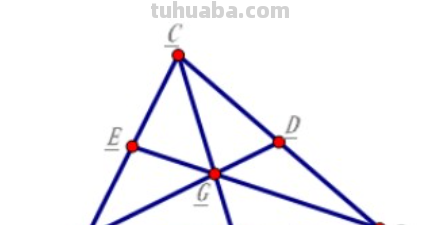
扩展资料：

证明一

1、重心到顶点的距离与重心到对边中点的距离之比为2：1。

例：已知：△ABC，E、F是AB，AC的中点。EC、FB交于G。

求证：EG=1/2CG

证明：过E作EH∥BF交AC于H。

∵AE=BE，搜衡EH//BF

∴AH=HF=1/2AF(平行线分线段成比例定理)

又∵ AF=CF

∴HF=1/2CF

∴HF:CF=1/2

∵EH∥BF

∴EG:CG=HF:CF=1/2

∴EG=1/2CG

方法二 连接EF

利用三角形相似

求证：EG=1/2CG 即证明EF=1/2BC

利用中位线可证明EF=1/2BC利用中位线可证明EF=1/2BC

2、重心和三角形3个顶点组成的3个三角形粗敏面积相等。

证明方法：

在△ABC内，三边为a，b，c，点O是该三角形的重心，世凳做AOA'、BOB'、COC'分别为a、b、c边上的中线。根据重心性质知：

OA'=1/3AA'

OB'=1/3BB'

OC'=1/3CC'

过O，A分别作a边上高OH'，AH

可知OH'=1/3AH

则，S△BOC=1/2×OH'a=1/2×1/3AHa=1/3S△ABC

同理可证S△AOC=1/3S△ABC

S△AOB=1/3S△ABC

所以，S△BOC=S△AOC=S△AOB

以上对于什么是三角形的重心的问题的6点解答，由涂画吧（tuhuaba.com）小编收集与互联网，希望对大家有用。