确定圆的条件 确定圆的条件教案

圆有两个要素：一个是圆心，另一个是半径，圆心确定圆的位置，半径确定圆的大小，作图的关键是确定圆心的位置和半径的大小。不在同一直线上的三个点确定一个圆。经过三角形各个顶点的圆叫做三角形的外接圆。

文章目录：

1. 确定圆的条件
2. 确定圆的条件有几个?
3. 确定圆的条件有哪些
4. 圆的确定条件
5. 确定圆的条件
6. 确定一个圆的两个基本条件

一、确定圆的条件

圆有两个要素：一个是圆心，另一个是半径，圆心确定圆的位置，半径确定圆的大小，作图的关键是确定圆心的位置和半径的大小。

不在同一直线上的三个点确定一个圆。

经过三角形各个顶点的圆叫做三角形的外接圆，外接圆的圆心叫做三角形的外心，这个三角形叫做圆的内接三角形。

锐角三角形的外心位于三角形内，直角三角形的外心位于直角三角形斜边中点，钝角三角形的外心位于三角形外。

圆的性质

1、圆是轴对称图形，其对称轴是任意一条通过圆心的直线。圆也是中心对称图形，其对称中心是圆心。

2、在同圆或等圆中，如果两个圆心角，两个圆周角，两组弧，两条弦，两条弦心距中有一组量相等，那么他们所对应的其余各组量都分别相等。

3、在同圆或等圆中，相等的弧所对的圆周角等于它所对的圆心角的一半（圆周角与圆心角在弦的同侧）。

4、如果一条弧的长是另一条弧的2倍，那么其所对的圆周角和圆心角是另一条弧的2倍。

二、确定圆的条件有几个?

圆内径是否一样！

确定圆的几何条件有：1，平面上有一个定点O，2，定长R，如果平面上的点到定点o的距离等于定长R，则这些点就组成圆。

就是圆心和半径啊

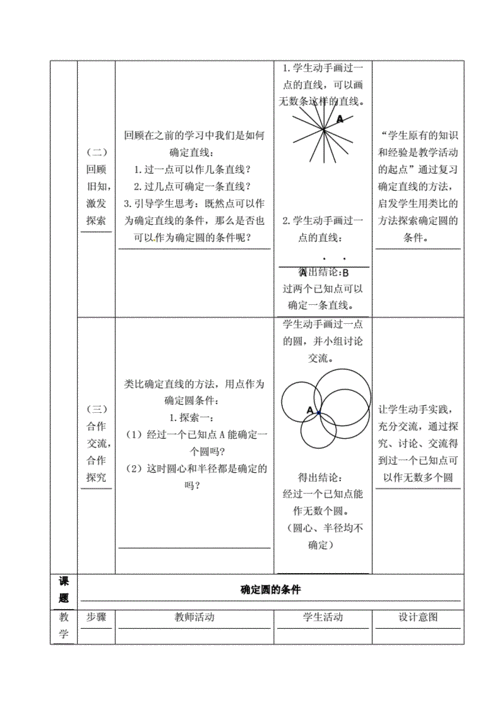
(1)三点定圆 确定圆的条件 类比确定直线的条件: 经过一点可以作无数条直线； 确定圆的条件 想一想,经过一点可以作几个圆?经过两点,三点,…,呢？ 确定圆的条件 2. 过已知点A,B作圆,可以作无数个圆. 确定圆的条件 3.作圆,使它过已知点A,B,C(A,B,C三点不在同一条直线上),你能作出几个这样的圆? 确定圆的条件 请你作圆,使它过已知点A,B,C(A,B,C三点不在同一条直线上). 以O为圆心,OA(或OB,或OC)为半径,作⊙O即可. 三点定圆 定理 不在一条直线上的三个点确定一个圆. 在上面的作图过程中.

三、确定圆的条件有哪些

　　确定圆的条件有两个：

　　1、平面上存在一个定点；

　　2、定长，平面上的点到定点的距离等于定长，则这些点组成圆。

　　总雀绝前结而言，顷清就是圆心和圆宏乱的半径。

四、圆的确定条件

1、能作出两个.

先作AB的中垂线L,然后以点A为圆心,以3cm长为半径作弧,交直线L于点M、N

,再分别以友纳M、N为圆心,3cm长为半径去作圆,所得到的圆即为所求.

2、经过不在同一条直磨搏线上的四个点不一定能瞎告祥作圆.

能做出来的常见的四边形有矩形,正方形等等.

五、确定圆的条件

1.可以做两个。

先做AB的中间垂线L，然后以A点为圆心，以3cm长的圆弧为半径，亮培物与直线L相交于M点和n点。

然后以m和n为圆心，3cm长为半径做一个圆，得到的圆就是你想要的。

2.通过不在同一直线上的四个点，不一定能做圆。

常见的可以做的四边形有长方形、正方形等等。

方法先从证明在同一圆内的四个点中选出三个点，再证明另一个点也在这个圆内。如果能证明这一点，就可以确认四个点在同一个圆内。

方法将证明为同心的四个点连接成两个同底三角形。如果能证明两个顶角是直角，就可以确认四点同心。

方法将证明为同心的四个点连接成两个同底边的三角形，两个三角形都在底边的同一侧。如果能证明顶角相等，就敬液能确认四点同心。

方法将证明同心的四个点连接成一个四边形。如果能证明它们的对角线是互补的，或者它们的一个外角等于它的相邻互补角的内对角线，就可以确认这四个点是同心的。

方法将被证明同心的四点连接成两条相交的线段，若能证明这两条线段除以交点的乘积相等，则可确认这四点同心；中歼或者连接被证明是同心的四个点，延伸相交的两条线段，如果能证明两条线段从交点到一条线段的两个端点的乘积等于两条线段从交点到另一条线段的两个端点的乘积，则可以确认这四个点也是同心的。

六、确定一个圆的两个基本条件

　在教学中，教师应指导学生自己去探索，与作直线类比，引出确定圆的条件问题，由易到难让学生经历作圆的过程，从中探索确定圆的条件．通过学生自己的亲身体验，再加上同学间的合作与交流，最后师生共同归纳总结便可轻松愉悦地完成 教学内容．

　　教学目标

　　（一）教学知识点

　　了解不在同行册一条直线上的三个点确定一个圆，以及过不在同一条直线上的三个点作圆的方法，了解三角形的外接圆、三角形的外心等概念．

　　（二）能力训练要求

　　1．经历不在同一条直线上的三个点确定一个圆的探索过程，培养学生的探索能力．

　　2．通过探索不在同一条直线上的三个点确定一个圆的问题，进一步体会解决 数学问题的策略．

　　（三）情感与价值观要求

　　1．形成解决问题的一些基本策略，体验解决问题策略的多样性，发展实践能力与创新精神．

　　2．学会与人合作 ，并能与他人交流思维的过程和结果．

　　教学重点

　　1．经历不在同一条直线上的三个 点确定一个圆的探索过程，并能掌握这个结 论．

　　2．掌握过不在同一条直线 上的三个点作圆的方法．

　　3．了解三角形的外接 圆、三角形的外心等概念．

　　教学难点

　　经历不在同一条直线上的三个点确定一个圆的探索过程，并能过不在同一条直线上的三个点作圆．

　　教学方法

　　教师指导学生自主探索交流法．

　　教具准备

　　投影片三张

　　第一张：（记作§ 3．4 A）

　　第二张：（记作§ 3．4 B）

　　第三张：（记作§ 3．4 C）

　　教学过程

　　Ⅰ．创设问题情境，引入新课 [师]我们知道经过一点可以作无数条直线，经过两点只能作一条直线，那么，经过一点能作几个圆？经过两点、三点……呢？本节课我们将进行有关探索．

　　Ⅱ．新课讲解

　　1．回忆及思考

　　投影片（§ 3．4 A）

　　1．线册敏段垂直平分线的性质及作法．

　　2．作圆的关键是什么？

　　[生]1．线段垂直平分线的

　　性质是：线段垂直平分线上的点

　　到线段两端点的距离相等．

　　作法：如右图，分别以A、B

　　为圆心 ，以大于 AB长为半径画弧，

　　在AB的两侧找出两交点C、D，作直线CD，则直线CD就是线段AB的垂直平分线，直线CD上的任一点到A与B的距离相等．

　　[师]我们知道圆的定义是：平面上到定点的距离等于定长的所有点组成的图形叫做圆．定点即为圆心，定长即为半径，根据定义大家觉得作圆的关键是什么？

　　[生]由定义可知，作圆的问题实质上就是圆心和半径的问题．因此作圆的关键是确定圆心和半径的大小．确定了圆心和半径，圆就随之确定．

　　2．做一做（投影片§3．4 B）

　　（1）作圆，使它经过已知点A，你能作出几个这样的圆？

　　（2）作圆，使它经过已知点A、B。你是如何作的`？你能作出几个这样的圆？其圆心的分布有什么特点？与线段AB有什么关系？为什么？

　　（3 ）作圆，使它经过已知点A、B、C（A、B、C三点不在同一条直线上）．你是档姿宏如何作的？你能作出几个这样的圆？

　　[师]根据刚才我们的分析已知，作圆的关键是确定圆心和半径，下面请大家互相交换意见并 作出解答．

　　[生]（1）因为作圆实质上是确定圆心和半径，要经过已知点A作圆，只要圆心确定下来，半径就随之确定了下来．所以以点A以外的任意一点为圆心，以这一点与点A所连的线段为半径就可以作一个圆．由于圆心是任意的．因此这样的圆有无数个，如图（1）．

　　（2）已知点A、B都在圆上，它们到圆心的距离都等于半径．因此圆心到A、B的距离 相等．根据前面提到过的线段的垂直平分线的性质可知，线段的垂直平分线上的点到线段两端点的距离相等，则圆心应在线段AB的垂直平分线上．在AB的垂直平分线上任意取一点，都能满足到A、B两点 的距离相等，所以在AB的垂直平分线上任取一点都可以作为圆心，这点到A的距离即为半径．圆就确定下来了．由于线段AB的垂直平分线上有无数点，因此有无数个圆心，作出的 圆有无数个．如图（2）．

　　（3）要作一个圆经过A、B、C三点，就是要确定一个点作为圆心，使它到三点的距离相等．因为到A、B两点距离相等的点的集合是线段AB的垂直平分线，到B、C两点距离相等的点的集合是线段BC的垂直平分线，这两条垂直平分线的交点满足到A、B、C三点的 距离相等，就是所作圆的圆心．

　　因为两条直线的交点只有一个，所以只有一个圆心，即只能作出一个满足条件的圆．

　　[师]大家的分析很有道理．究竟应该怎样找圆心呢？

　　3．过不在同一条直线上的三点作圆．

　　投影片（§3．4 C）

　　作法 图示

　　1．连结AB、BC

　　2．分别作AB、BC的垂直平分线DE和FG，DE和FG相交于点O

　　3．以O为圆心，O A为半径作圆⊙O就是所要求作的圆

　　他作的圆符合要求吗？与同伴交流．

　　[生]符合要求．

　　因为连结AB，作AB的垂直平分线ED，则ED上任意 一点到A、B的距离相等，连结BC，作BC的垂直平分线FG，则FG上的任一点到B、C的距离相等．ED与FG的交点O满足OA=OB=OC，因此这样的画法满足条件．

　　[师]由上可知，过已知一点可作无数个圆，过已知两点也可作无数个圆，过不在同一条直线上的三点可以作一个圆，并且只能作一个圆．

　　不在同一直线上的三个点确定一个圆．

　　4．有关定义

　　由上可知，经过三角形的三个顶点可以

　　作一个圆，这个圆叫做三角形的外接圆（circumcircle of triangle）．这个三角：形叫这个圆的内接三角形．

　　外接圆的圆心是三角形三边垂直平分线的交点，叫做三角形的外心（circumcenter）．

　　Ⅲ．课堂练习

　　已知锐角三角形、直角—三角形、钝角三角形，分别作出它们的外接圆．它们外心的位置有怎样的特点？

　　解：如下图．

　　锐角三角形 直角三角形 钝角三角形

　　O为外接圆的圆心，即外心．

　　锐角三角形的外心在三角形的内部，直角三角形的外心在斜边上， 钝角三角形的外心在三角 形的外部．

　　Ⅳ．课时小结

　　本节课所学内容如下：

　　1．经历 不在同一条直线上的三个点确定一个圆的探索过程．

　　2．过不在同一条直线上的二个点作圆的方法．

　　3．了解三角形的外接圆，三角形的外心等概念．

以上对于确定圆的条件的问题的6点解答，由涂画吧（tuhuaba.com）小编收集与互联网，希望对大家有用。