三角形中点连线的性质 等边三角形中点连线的性质

中线的性质：对于三角形而言，三角形的中线是连接三角形的一个顶点及其对边中点的线段，一个三角形有3条中线。主要有以下一些性质：1、任意三角形的三条中线把三角形分成面积相等的六个部分。

文章目录：

1. 三角形中线的性质是什么?
2. 三角形中线的性质是什么?
3. 三角形中线定理和性质
4. 三角形中线的性质是什么?
5. 三角形中线的性质是什么?

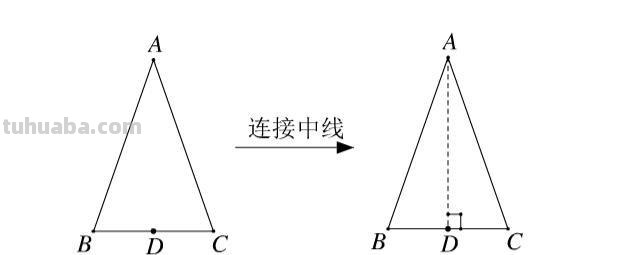
一、三角形中线的性质是什么?

简单分析一下，详情如图所示

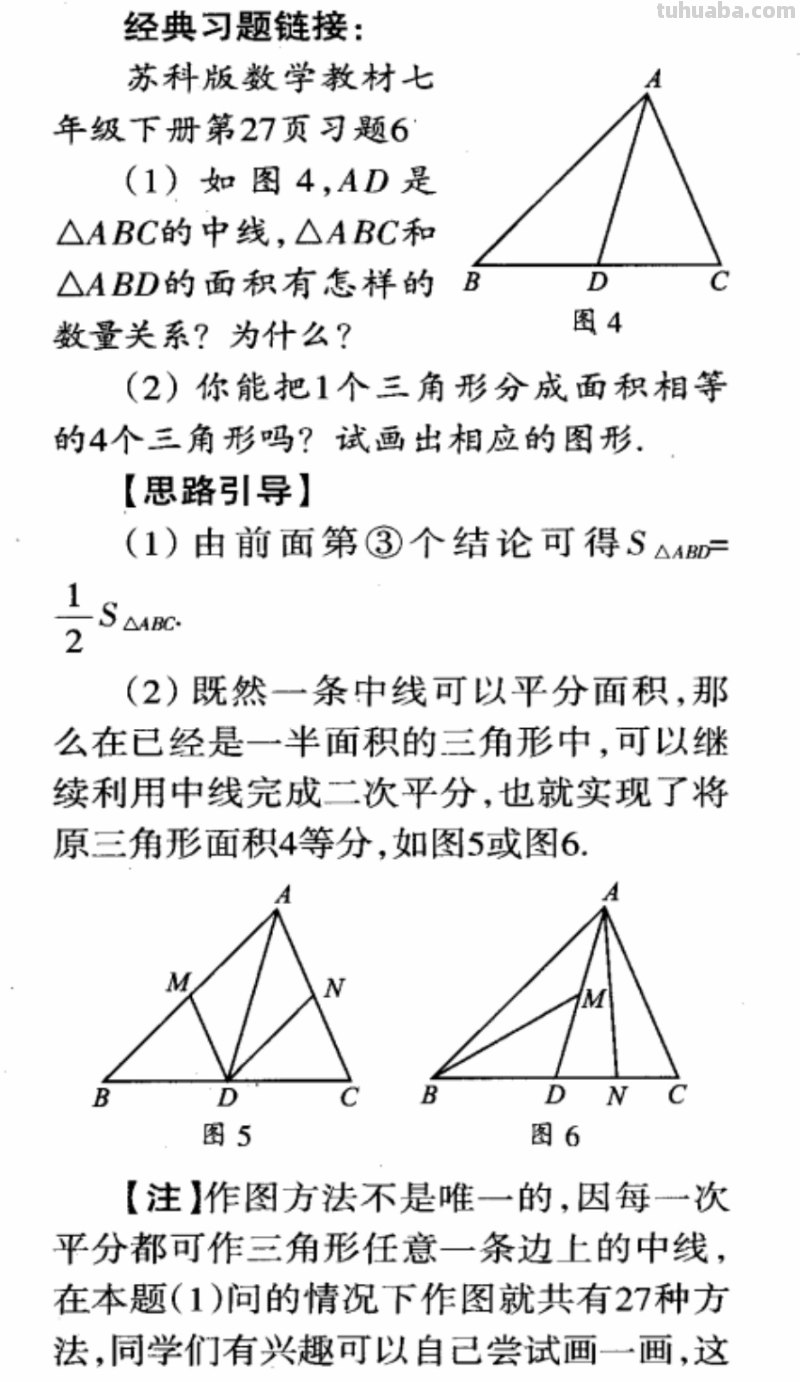
中线的性质：

对于三角形而言，三角形的中线是连接三角形的一个顶点及其对边中点的线段，一个三角形有3条中线。主要有以下一些性质：

1、任意三角形的三条中线把三角形分成面积相等的六个部分。中线都把三角形分成面积相等的两个部分。除此之外，任何其他通过中点的直线都不把三角形分成面积相等的两个部分。

2、三角形中中线的交点为重心，重心分中线为2：1（顶点到重心：重心到对边中点）。

3、在一个直角三角形中，直角所对应的边上的中线为斜边的一半。

三角形中线的判断方法：

1、根据定义：三角形两边中点之间的线段为三角形的中位线。

2、经过三角形一边中点与另一边平行的直线与第三边相交,交点与中点之间的线段为三角形的中位线。

3、端点在三角形的两边上与第三边平行且等于第三边的一半的线段为三角形的中位线。

二、三角形中线的性质是什么?

简单分析一野判哗下颂行，详情如冲宽图所示

三角形中线的性质是：

1、三角形的三条中线都在碧穗仔三角形内。

2、三角形的三条中线交于一点，该点叫做三角形的重心。

3、直角三角形斜边上的中线等于斜边的1/2。

4、三角形中线组族游成的三角形面积等于这个三角形面积的3/4；5、三角形重心将中线分为长度比为1:2的两条线段。

中线是三角形中从某边的中点连向对角的顶点的线段。 

三角形的三条中线总是相交于同一点，这个点称为三角形的重心，重心分中线为2：1（顶点到重心：重心到对边中点）。

中线的性质：

1、任意三角形的三条中线把三角形分成面积相等的六个部分。中线都把三角形分成面积相等的两个部分。除此之外，任何其他通过中点的直线都不把三角形分成面积相等的两个部分。 

2、三角形中中线的交点为重心，重心分中线为2：1（顶点到重心：重心到对边中点）。

3、在一个直角三角形中，直角所对应的边上的中线为斜边的一半。

中线的做用：

1、中线的作用在于当负载不对称时，保证各相电压仍然对称，都能正常工作；如果一相发生断线，也只影响本相负载，而不影响其它两相负载。

2、任意三角形的三条中线把三角形分成面积相等的六个部分。

3、是平分对边，还可以把三角形分为面积相等的两悔汪部分，用来求证全等三角形，三角形的中线是连接三角形的一个顶点及对边的线段，一个三角形有3条中线。

三、三角形中线定理和性质

三角形中线性质定理：

1.三角形的三条中线都在三角形内。

2.三角形的三条中线交于一点，该点叫做三角形的重心。

3.直角三角形斜边上的中线等于斜边的一半。

4.三角形中线组成的三角形面积等于这个三角形面积的3/4.

在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线。

由于三角形有三条边，所以一个三角形有三条中线。

且三条中线交于一点。这点称为三角形的重心。

每条三角形中线分得的两个三角形面积相等。

三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线。

三角形的角平分线不是角的平分线，是线段。角的平分线是射线。（这是三角形的角平分线与角平分线的区别）

四、三角形中线的性质是什么?

三角形中线的性质：三角形的三条中线都在三角形内，三角形的三条中线交于一点，该点叫做三角形的重咐告陵心，直角三角形斜边上的中线等于斜边的1/2，三角形重心将中线分为长度比为1：2的两条线段等。

三角形有四线，分别为中线，高，角平分线，中友敬位线：

1、中线定义：三角形的中线是连接三角形的一个顶点及其对边衡戚中点的线段，一个三角形有3条中线。

2、高定义：从一个顶点向它的对边所在的直线画垂线，顶点和垂足之间的线段。

3、角平分线定义：三角形一个内角的平分线与这个角的对边相交，这个角的顶点与交点之间的线段。

4、中位线定义：三角形的三边中任意两边中点的连线。

五、三角形中线的性质是什么?

三角形中线的性质：三角形的三条中线都在三角形内；三角形的三条中线交于一点，该点叫做三角形的重心；直角三角形斜边上的中线等于斜边的1/2；三角形重心将中线分为长度比为1：2的两条线段等。

△中线性质

设△ABC的角A、角B、角C的对边分别为a,b,c。

1、三角形的三条中线都在三角形内。

2、三角形的三条中线长：

ma=(1/2)√（2b²+2c²-a²）

mb=(1/2)√（2a²+2c²-b²）

mc=(1/2)√（2a²+2b²-c²）

(ma、mb、mc分别为角A,B,C所对边的中线长）

3、三角形的三条中线交于一点，该点叫做三角形的重心。

4、直角三角形斜边上的中线等于斜边的1/2。

5、角形中线组成的三角形面积等于这个三角形面积的3/4。

6、三角形重心将中线分为长度比为1:2的两条线段。

三角形的中线是接三角形顶点和它的对边中点的线段。每个三角形都有三条中线，它们都在三角形的内部 [1]  。在三角形中，三条中线的交点是三角形的重心。三角形的三条中线交于一点，这点位于各中线的三分之二处。

设△ABC的角A、角B、角C的对边分别为a,b,c。

1、三角形的三条中线都在三角形内。

2、三角形的三条中线长：

(ma、mb、mc分别为角A,B,C所对边的中线长）

3、三角形的三条中线交于一点，该点叫做三角形的重心。

4、直角三角形斜边上的中线等于斜边的1/2。

5、三角形中线组成的三角形面积等于这个三角形面积的3/4。

6、三角形重心将中线分为长度比为1:2的两条线段 。

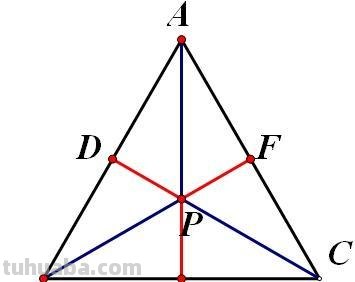
“中心”与“重心”很容易弄混淆，“中心”只存在于正三角形，也就是等边三角形当中。在等边三角形中，其内心，外心，重心，垂心都在一个点上，于是称之为中心。

内心：三角形的内心是三角形三条内角平分线的交点。

外心：三角形三条边的中垂线的交点叫作三角形的外心，即外接圆圆心 [2]  。

重心：三角形三条中线的交点叫作三角形的重心。

垂心：三角形三条垂线的交点叫作三角形的垂心。

如图1所示，BF,CD,AE分别为正三角形ABC的三条高，中线，角平分线，其交点P即为正三角形ABC的中心。

以上对于三角形中点连线的性质的问题的5点解答，由涂画吧（tuhuaba.com）小编收集与互联网，希望对大家有用。